Introduction
In this blog post, I will embark on a journey into the world of machine learning, specifically classification, using a real-world dataset – the Breast Cancer Wisconsin dataset. The goal is to build a classification model that can predict whether a breast tumor is benign (a benign tumor is a non-cancerous growth of cells) or malignant (cancerous growths, life-threatening) based on a set of features derived from cell nuclei characteristics.
I’ll be using one of the most popular machine-learning libraries in Python, Scitkit-Learn, which provides a comprehensive set of tools for machine learning.
Throughout this blog post, I will cover the following key points: (1) Data Exploration, (2) Model Building, (3) Model Evaluation, (4) KNN Tuning, and (5) Model Improvement.
1.0 Data Exploration
We’ll start by exploring the Breast Cancer Wisconsin dataset, gaining an understanding of its structure, and the meaning of each feature. We’ll use Seaborn to visualize the data, uncover patterns, and get a feel for the dataset.
To learn more about the datasets, including documentation and definitions of each column, visit Kaggle.
from sklearn.datasets import load_breast_cancer
import pandas as pd
import numpy as np
############################################
# STEP 1: LOAD & EXPLORE DATASET
############################################
# Load the Breast Cancer Wisconsin dataset
data = load_breast_cancer()
# Convert the dataset into a Pandas DataFrame for easier exploration
df = pd.DataFrame(np.c_[data.data, data.target], columns= list(data.feature_names) + ['target'])
# Get the shape of the dataset (number of rows and columns)
print("Shape of the dataset:", df.shape)
----------------- OUTPUT -----------------------
Shape of the dataset: (569, 31)
------------------------------------------------
# Count the number of samples for each class in the target variable
print("Class distribution:")
print(df['target'].value_counts())
----------------- OUTPUT -----------------------
Class distribution:
1.0 357
0.0 212
------------------------------------------------
# Check for missing values in the dataset
print("Missing values:")
print(df.isnull().sum())
----------------- OUTPUT -----------------------
Missing values:
mean radius 0
mean texture 0
mean perimeter 0
mean area 0
...
target 0
------------------------------------------------
Observations:
- There are two target variables, which are binary (0 for benign and 1 for malignant).
- There are 569 rows and 31 columns in the dataset.
- There are 357 rows where the target is 1 and 212 rows where the target is 0.
- There are no missing values in the dataset.
import seaborn as sns
sns.pairplot(df, hue="target", vars=['mean radius', 'mean texture', 'mean area'], palette="husl")
plt.show()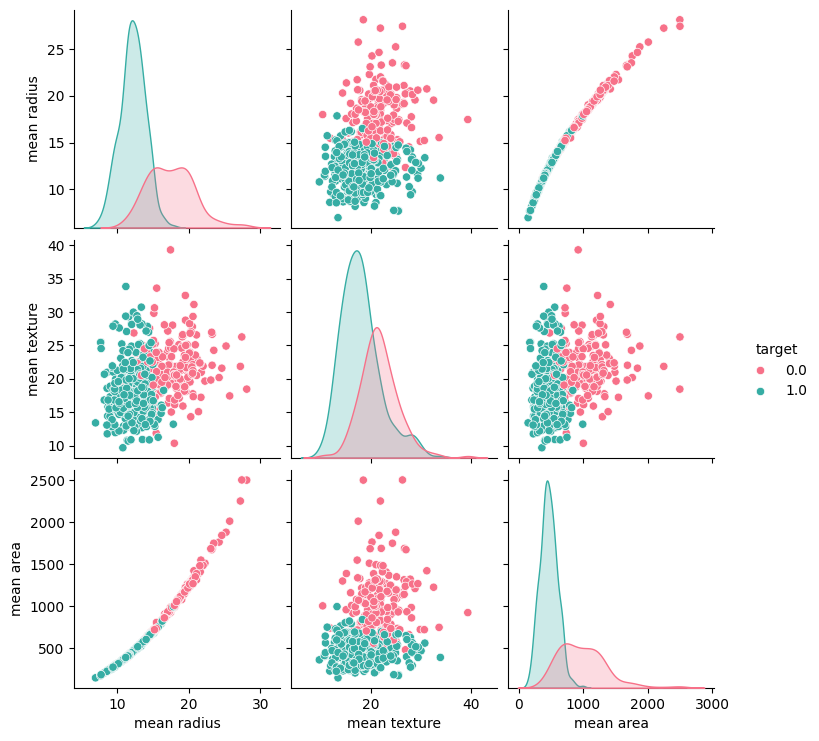
The code above generates a part plot using Seaborn for three specific (“mean radius,” “mean texture,” and “mean area”) from the Breast Cancer Wisconsin dataset. This pair plot is color-coded by the target variable, which indicates whether tumors are benign or malignant (0 for benign and 1 for malignant).
By examining the scatter plots, we can look for clusters, patterns, and separations between the two classes (benign and malignant tumors).
Observations:
- Examining the scatter plot located in the bottom-left corner, we can observe that when the “mean radius” is less than ~17 and the “mean area” is under 1000, there’s a higher likelihood of the tumor being classified as malignant (1).
- Analyzing the chart displayed above the chart mentioned is the prior observation, it becomes apparent that when the “mean radius” is less than 17, the likelihood of malignancy is evident. However, the role of “mean texture” in determining malignancy is less discernible when its value is either 0 or 1.
2.0 Model Building
Following the Data Exploration step, we transition into the model-building phase. Here, we employ the scikit-learn library to create a KNN classifier. The dataset is divided into a training set and a testing test using train_test_split function.
The KNN classifier is then instantiated with a specified number of neighbors (k), in this case, set to 5. The model is trained on the training data, and predictions are made on the test data.
############################################
# STEP 2: MODEL BUILDING
############################################
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
X = data.data # Features
y = data.target # Target labels
# Split the dataset into a training set and a testing set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create a KNN classifier
knn = KNeighborsClassifier(n_neighbors=5) # You can adjust the number of neighbors (k) as needed
# Train the model on the training data
knn.fit(X_train, y_train)
# Make predictions on the test data
y_pred = knn.predict(X_test)3.0 Model Evaluation
After creating the KNN model, we assess the performance of the KNN model. Model evaluation is crucial to determine how well the model generalizes on unseen data and how accurately it classifies breast tumors as benign or malignant. The evaluation metrics help us gain insights into the model’s strengths and limitations.
############################################
# STEP 3: MODEL EVALUATION
############################################
# Evaluate the model
accuracy = accuracy_score(y_test, y_pred)
confusion = confusion_matrix(y_test, y_pred)
report = classification_report(y_test, y_pred)
# Print the results
print("Accuracy:", accuracy)
print("Confusion Matrix:\n", confusion)
print("Classification Report:\n", report)
----------------- OUTPUT -----------------------
Accuracy: 0.956140350877193
Confusion Matrix:
[[38 5]
[ 0 71]]
Classification Report:
precision recall f1-score support
0 1.00 0.88 0.94 43
1 0.93 1.00 0.97 71
accuracy 0.96 114
macro avg 0.97 0.94 0.95 114
weighted avg 0.96 0.96 0.96 114
------------------------------------------------Observations:
- Accuracy: 0.956140350877193
- Accuracy is a measure of how many predictions the model got correct out of the total predictions made. In this case, the accuracy is approximately 95.61%, indicating that the model correctly classified about 95.61% of the data points.
- Confusion Matrix:
- A confusion matrix is a table that describes the performance of a classification model. It provides information about the true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN). In this case, the confusion matrix is as follows:
- True Positives (TP): 71 cases were correctly classified as Class 1.
- True Negatives (TN): 38 cases were correctly classified as Class 0.
- False Positives (FP): 5 cases were incorrectly classified as Class 1 when they were actually Class 0.
- False Negatives (FN): 0 cases were incorrectly classified as Class 0 when they were actually Class 1.
- A confusion matrix is a table that describes the performance of a classification model. It provides information about the true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN). In this case, the confusion matrix is as follows:
- Classification Report:
- The classification report provides a summary of various metrics for each class (Class 0 and Class 1) and overall performance:
- Precision: The precision measures the proportion of true positive predictions out of all positive predictions made by the model. For Class 0, the precision is 1.00, indicating that when the model predicts Class 0, it is highly likely to be correct. For Class 1, the precision is 0.93, indicating that when the model predicts Class 1, it is correct in 93% of cases.
- Recall (Sensitivity): The recall measures the proportion of true positive predictions out of all actual positives in the dataset. For Class 0, the recall is 0.88, meaning that the model correctly identifies 88% of actual Class 0 instances. For Class 1, the recall is 1.00, indicating that the model correctly identifies all actual Class 1 instances.
- F1-Score: The F1-score is the harmonic mean of precision and recall, providing a balance between these two metrics. For Class 0, the F1-score is 0.94, and for Class 1, it is 0.97. The weighted average F1-score (0.96) accounts for the class distribution in the dataset.
- Support: The support represents the number of instances in each class in the dataset.
- The classification report provides a summary of various metrics for each class (Class 0 and Class 1) and overall performance:
Overall, these evaluation metrics suggest that the KNN model is performing well, with high accuracy, good precision, recall, and F1-scores for both classes.
4.0 KKN Tuning
We saw above that using 5 neighbors resulted in an accuracy score of 0.9561, but is 5 neighbors the optimal number?
One of the essential aspects of optimizing a machine learning model is tuning its hyperparameters. The n_neighbors hyperparameter plays a significant role in KNN, as it determines how many nearest data points should be considered when making predictions. While we initially trained the model with 5 neighbors, we recognize that this may not be the optimal number.
To make the performance evaluation more accessible and visually informative, we employ Matplotlib. We record and compare the accuracy of the model on both the training and testing data for different values of n_neighbors. These accuracy values are then visualized in a plot, providing a clear depiction of how the model’s accuracy behaves as we adjust the number of neighbors.
############################################
# STEP 4: MODEL IMPROVEMENT
############################################
import matplotlib.pyplot as plt
# Initialization
train_accuracies = {}
test_accuracies = {}
neighbors = np.arange(1,26)
# Iterating over n_neighbors
for neighbor in neighbors:
knn = KNeighborsClassifier(n_neighbors=neighbor) # Use 'neighbor' for the number of neighbors
knn.fit(X_train, y_train)
train_accuracies[neighbor] = knn.score(X_train, y_train)
test_accuracies[neighbor] = knn.score(X_test, y_test)
# Extract the accuracy values from the dictionaries
train_accuracy_values = [train_accuracies[neighbor] for neighbor in neighbors]
test_accuracy_values = [test_accuracies[neighbor] for neighbor in neighbors]
# Create a plot
plt.figure(figsize=(10, 6))
plt.plot(neighbors, train_accuracy_values, label="Train Accuracy", marker='o')
plt.plot(neighbors, test_accuracy_values, label="Test Accuracy", marker='o')
plt.title('KNN Accuracy for Different Values of n_neighbors')
plt.xlabel('n_neighbors')
plt.ylabel('Accuracy')
plt.xticks(neighbors)
plt.legend()
plt.grid(True)
plt.show()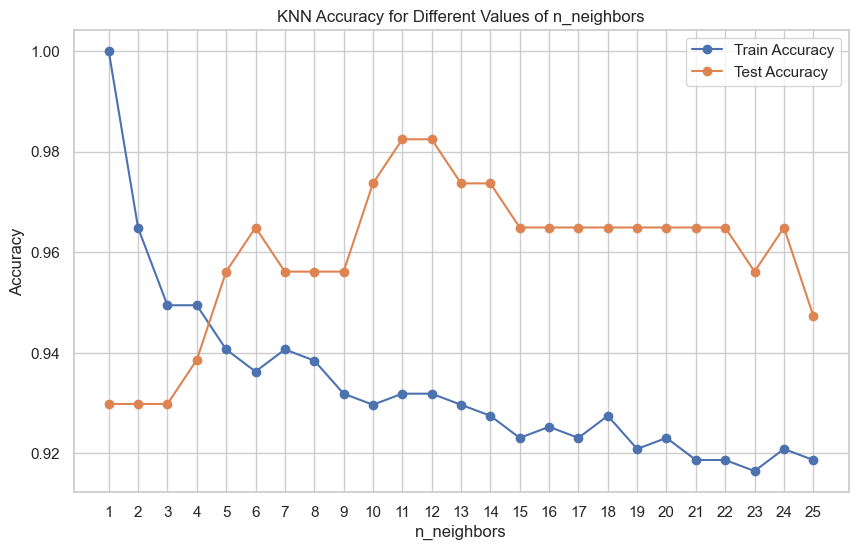
As seen in the chart above, as we increase n_neighbors, the training accuracy gradually decreases, which is expected because with more neighbors, the model generalizes better and is less prone to overfitting.
Test accuracy tends to increase as n_neighbors increases, peaking at a certain point and then possibly decreasing if the model becomes too biased.
When n_neighbors is very low (e.g., 1 or 2), the model overfits the training data, resulting in high training accuracy but lower test accuracy. It means the model is too sensitive to noise in the training data.
There is a sweet spot for n_neighbors around 11 or 12 where the test accuracy is maximized. This is the point where the model generalizes well to unseen data without underfitting or overfitting.
As we increase n_neighbors beyond the optimal value, test accuracy tends to stabilize or slightly decrease, indicating that the model may become overly biased and start to underfit.
In this case, n_neighborsof 11 or 12 appears to be a good choice, as it provides the highest test accuracy and a reasonable training accuracy.
5.0 Model Improvement
By modifying the code to set the number of neighbors to 11, we see an improved accuracy score from 0.9561 using 5 neighbors, to 0.9824 using 11 neighbors. This change enhances the model’s ability to make accurate predictions based on the nearest data points in the feature space.
############################################
# STEP 5: OPTIMAL KNN MODEL
############################################
X = data.data # Features
y = data.target # Target labels
# Split the dataset into a training set and a testing set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create a KNN classifier
knn = KNeighborsClassifier(n_neighbors=11)
# Train the model on the training data
knn.fit(X_train, y_train)
# Make predictions on the test data
y_pred = knn.predict(X_test)
# Evaluate the model
accuracy = accuracy_score(y_test, y_pred)
confusion = confusion_matrix(y_test, y_pred)
report = classification_report(y_test, y_pred)
# Print the results
print("Accuracy:", accuracy)
print("Confusion Matrix:\n", confusion)
print("Classification Report:\n", report)
----------------- OUTPUT -----------------------
Accuracy: 0.9824561403508771
Confusion Matrix:
[[41 2]
[ 0 71]]
Classification Report:
precision recall f1-score support
0 1.00 0.95 0.98 43
1 0.97 1.00 0.99 71
accuracy 0.98 114
macro avg 0.99 0.98 0.98 114
weighted avg 0.98 0.98 0.98 114
------------------------------------------------
6.0 Conclusion
We began by delving into the Breast Cancer Wisconsin dataset during the Data Exploration step, gaining insights into its structure and uncovering distinctive patterns. Following this, we harnessed the K-Nearest Neighbors (KNN) algorithm, renowned for its simplicity and efficacy in classification tasks. Our model was trained on the training data and applied to make predictions on the test data.
Following this, we carried out a model evaluation of the model’s performance, an essential step to grasp its strengths and limitations. This assessment yielded an accuracy score of 95.61%. In our pursuit of optimization, we thoroughly examined the model’s performance by experimenting with different values of n_neighbors. Through this exploration, we determined that configuring n_neighbors to 11 was the most effective choice. Implementing this adjustment led to a model refinement, significantly boosting the accuracy score to an impressive 98.24%.
It is important to consider the model’s limitations, such as:
- Model Selection: While KNN is used in this analysis, other machine learning algorithms could be more suitable for this specific task. A broader exploration of different models and techniques may yield better results, such as Logistic Regression, Decision Trees, Support Vector Machines (SVM), and Naive Bayes.
- Feature Selection: The dataset contains a relatively large number of features (30 features) which were all used in the model. Feature selection or dimensionality reduction techniques may be necessary to identify the most relevant features for classification. High-dimensional data can lead to overfitting.
- Generalization: While the K-Nearest Neighbors (KNN) model might perform well on this dataset, its generalization to other datasets or real-world clinical scenarios may be limited. It’s essential to evaluate models in various contexts to ensure their broader applicability.
- Data Quality: Although this dataset is considered clean, real-world healthcare data can be noisy and contain missing values. Preprocessing healthcare data can be a challenging task, and the quality of the data can significantly impact model performance.